Competition Task
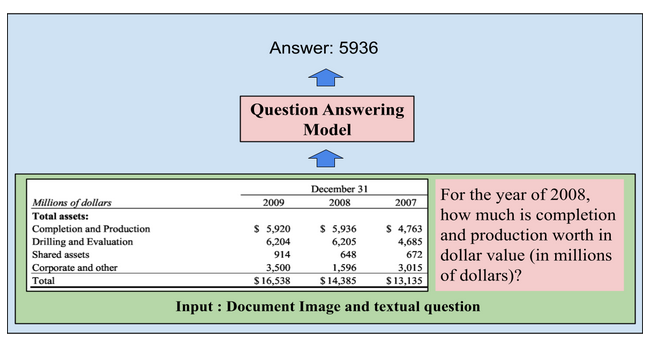
Given a document image and questions, the task of the competition is to produce answers corresponding to the questions. For example
Evaluation
During the evaluation, it is expected that a model will take only the document image and question as the input to produce the output. This output is then compared against the ground truth answer to obtain a quantitative evaluation score computed over the entire test dataset.
In most cases, the expected answers to questions from business documents are single numeric token ones. It makes classical accuracy a good prospect for evaluating this task. While for a more generic assignment of visual question answering, there may be some subjectivity in the answers (e.g., white, off-white, and cream may all be correct answers), the solutions for the proposed task are primarily objective and absolute. It makes evaluation relatively straightforward. Hence, we use standard accuracy as the primary criterion for evaluation. Further, for numeric-type answers, we also employ averaged absolute deviation as one of the criteria.
However, since the input to the model will only be by the document image to answer a specific query, it is not fair to penalise the VQA model word/token detection and recognition. Therefore, we also employ Averaged Normalised Levenshtein Similarity (ANLS) as proposed in DocVQA [2, 3], which responds softly to answer mismatches due to OCR imperfections.
ANLS is given by equation 1, where N is the total number of questions, M are possible ground truth answers per question, \(i = {0...N}\), \(j = {0...M}\) and \( o_{q_i}\) is the answer to the \( i^{th} \) question \( q_i\)
$$ \begin{equation} \label{eq1} \begin{split} ANLS & =\frac{1}{N}\sum_{i=0}^{N}\Big( \max_j\ s(a_{ij}, o_{q_i}) \Big) \\ s(a_{ij}, o_{q_i}) & = \begin{cases} 1 - NL(a_{ij}, o_{q_i}), & \text{if $NL(a_{ij}, o_{q_i})<\tau$}.\\ 0, & \text{otherwise}. \end{cases} \end{split} \end{equation} $$ where \( NL(a_{ij}\) , \(o_{q_i} )\) is the normalized Levenshtein distance (ranges between 0 and 1) between the strings \( a_{ij}\) and \( o_{q_i}\). The value of \(\tau\) can be set to add softness toward recognition errors. If the normalized edit distance exceeds \(\tau\), it is assumed that the error is because of an incorrectly located answer rather than an OCR mistake.